

Di seguito riportiamo gli aspetti peculiari dell'algoritmo di starburst. Per ulteriori approfondimenti: "Starburst: A hybrid algorithm for video-based eye tracking combining feature-based and model-based approaches" di Dongheng Li, David Winfield, Derrick J. Parkhurst.
Esistono diverse tecniche per la tracciatura oculare, tra le quali è stato scelto l’algoritmo di starburst che presenta il giusto compromesso tra accuratezza e velocità di esecuzione. Questa implementazione si basa sull’elaborazione di immagini acquisite da una videocamera illuminando opportunamente l’occhio con led a infrarossi per aumentare il contrasto tra pupilla e sclera. Gli infrarossi inoltre non disturbano in alcun modo la visuale di un osservatore. Un possibile svantaggio di questo approccio è il fatto che la tecnica a infrarossi è tale da non poter essere utilizzata in luoghi aperti a causa dell'interferenza della luce solare.
Le operazioni presentate qui di seguito sono eseguite su ogni frame catturato dalla videocamera.
Per quanto riguarda la riduzione del rumore è stato eseguito un filtraggio gaussiano per eliminare il rumore shot e successivamente viene eliminato il rumore di linea effettuando un'opportuna normalizzazione attraverso la seguente relazione:
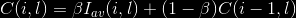
dove Iav(i,l) è l’intensità media della linea l per il frame i-esimo e ß=0.2. Per i=1 si assume C(i,l)=I(i,l).
La tecnica adottata causa delle piccole aree molto luminose dovute ai fasci di infrarossi che si riflettono sull’occhio, pertanto è necessario rimuovere tali riflessi per una migliore individuazione della pupilla: per la localizzazione è stata utilizzata una tecnica a soglia adattativa, limitando la ricerca ad una regione di interesse vicina alla pupilla. Inizialmente viene applicata una soglia massima per ottenere un’immagine binaria nella quale solo i pixel con intensità maggiore della soglia sono candidati per essere punti del riflesso della cornea. Quindi la soglia viene progressivamente diminuita e, di volta in volta, viene calcolato il rapporto tra la più grande area corrispondente ad un candidato riflesso della cornea e la media di tutte le altre regioni candidate. L’intensità del riflesso decresce monotonicamente muovendosi verso il suo contorno e la soglia ottima risulta quella che massimizza il rapporto precedentemente citato. Il riflesso della cornea viene localizzato come il centro della regione più estesa. Questo procedimento tuttavia non permette di individuare l’intero profilo, pertanto viene utilizzato il metodo di ricerca Nelder-Mead Simplex per trovare il raggio del riflesso della cornea scegliendo quello che minimizza:
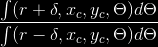
Infine il riflesso viene eliminato tramite interpolazione radiale colorando ogni pixel del riflesso con l’intensità media del contorno della regione.

Procedimento di localizzazione e rimozione del riflesso della cornea.
L'individuazione comincia a partire da un punto determinato dall'interazione iniziale dell'utente (click al centro della pupilla). Da questo punto il software procede muovendosi lungo N raggi calcolando, di volta in volta, la derivata dell’intensità di due punti adiacenti lungo il raggio. Quando questa derivata supera la soglia si è in corrispondenza di un probabile punto del contorno: questa è la tecnica con cui viene determinato un primo set di candidati. Per ogni punto di questo set viene successivamente percorso il raggio in direzione opposta e, in modo analogo, si determina un ulteriore gruppo di candidati. Il nuovo punto di partenza viene allora ricalcolato come la media dei punti costituenti i set precedenti e il processo complessivo termina quando il punto converge: questa analisi a due stadi aumenta la robustezza del metodo.

Localizzazione del primo set di punti del contorno della pupilla.

Localizzazione del secondo set di punti del contorno della pupilla.
A questo punto è possibile, partendo dai candidati appena trovati, utilizzare l’algoritmo RANSAC per trovare l’ellisse che meglio approssima il contorno della pupilla. Questo algoritmo consente di ottenere risultati migliori rispetto al metodo dei minimi quadrati, in quanto distingue gli inliers dagli outliers e inoltre lavora su un set ridotto di dati. In particolare vengono scelti iterativamente cinque punti casuali tra quelli candidati ai quali viene applicata la decomposizione a valori singolari (SVD) per individuare i coefficienti dell’ellisse. A questo punto del flusso di elaborazione, se viene individuata un’elisse reale l’algoritmo procede comunicando i parametri altrimenti si ripete il procedimento: i punti del contorno trovati nella fase precedente che appartengono (entro una certa tolleranza) all’ellisse appena ottenuta tramite la SVD costituiscono un consenus set.
Al passaggio del mouse il diagramma si ingrandisce

Questo procedimento viene ripetuto per R iterazioni e l’ellisse che meglio approssima il modello è quella costituita dal consensus set col maggior numero di punti. Gli inliers sono determinati come i punti per i quali la distanza euclidea dal centro dell’ellisse è minore di una data soglia, che può essere ricavata tramite un modello probabilistico. Assumendo che la varianza media dell’errore sia approssimativamente 1 pixel e supponendo che questo errore abbia una distribuzione gaussiana a media nulla, la soglia può essere determinata da una distribuzione Χ2 con un grado di libertà. Ciò porta ad una distanza soglia di 1.95959 pixel. Per avere una probabilità p=0.99 che il sottogruppo selezionato casualmente contenga solo inliers il numero di iterazioni deve essere:
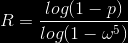
dove ω è la proporzione di inliers nel campione. Sebbene ω non sia nota a priori, è limitata inferiormente dal massimo consensus set. Siccome R può essere inizialmente molto grande, man mano che le iterazioni procedono si stimano nuovamente i parametri del modello ogni volta che si trova un consensus set di dimensioni maggiori fino a quando il numero di inliers rimane costante.